Gaussian Process Background

Introduction

This document focuses on the implementation details of some of the approaches used in albatross. For a deep dive in Gaussian processes you’re probably better off reading the book Gaussian Processes for Machine Learning. There are also a number of excellent introductions to Gaussian processes (see our References) here we assume some understanding of GPs and focus on describing the details of the implementations we use in albatross.

Notation

For the most part the notation below tries to stay as close as possible to the notation used in Gaussian Processes for Machine Learning, but there are a few departures.

In general a bold font variable such as \(\mathbf{y}\) indicates a random variable and the non bold font equivalent, \(y\), indicates a realization of that variable. Note that this differs from the popular notation of using bold font for vectors, for most of what follows we assume that whether something is a scalar or a vector needs to be inferred from context. As an example, if \(\mathbf{y} \sim \mathcal{N}(0, 1)\) then one measurement, \(y\), from the distribution \(\mathbf{y}\) might be \(0.83\). To be explcit that a sample came from a distribution we’d write \(y \leftarrow \mathbf{y}\).

Conditional distributions are written with the \(|\) symbol so, for example, the random variable \(\mathbf{z}\) given knowledge that \(\mathbf{y}\) is \(y\) would be written, \(\mathbf{z}|\mathbf{y}=y\). Often this is shortened to \(\mathbf{z} | y\). If we really want to be clear about something being a random variable we’ll write \(\mbox{p}( \mathbf{z}|y)\).

Gaussian Process Regression

Gaussian processes can be used for many different prediction problems but here we focus on regression, which refers to a situation where you have some noisy observations of a function and you’d like to infer the function value at un-observed locations.

More specifically, say you have some training data, \(\mathcal{D} = \left\{(x_i, y_i); i \in [0, \ldots, n]\right\}\) which consists of measurements \(y_i\) of the unknown function, \(f\), evaluated at \(x_i\), which is contaminated by noise, \(\mathbf{\epsilon}_i \sim \mathcal{N}\left(0, \sigma_i^2\right)\),

\[y_i \leftarrow f(x_i) + \mathbf{\epsilon}_i\]

Gaussian process regression is used to infer the unknown function given the noisy measurements. The result is a function, \(f_{GP}\left(x^*\right)\) which provides us an estimate of the unknown function. The use of \(*\) indicates out of sample locations, meaning locations which were not neccesarily used to train the Gaussian process. Predictions from a Gaussian process provide more than just the expected value of the unknown function, it provides an estimate of the full distribution of possible function values,

\[f_{GP}\left(x^*\right) \rightarrow \mbox{p}\left(f(x^*)|\mathcal{D}\right).\]

Covariance Functions

We describe a Gaussian process as,

\[f_{GP}\left(x\right) \sim \mathcal{GP}\left(m(x), c(x, x')\right).\]

Here \(m(x)\) is the mean function which computes the prior estimate of the function at arbitrary locations and \(c(x, x')\) is the covariance function (aka kernel) which defines the covariance between two measurements at locations \(x\) and \(x'\). Note that usually the mean is set to zero since these effects can be removed before modelling or can be folded into the covariance function.

Gaussian process model development is usually focused on defining the covariance function. The covariance function describes our prior expectations about what the unknown function might look like. Covariance functions can be designed to capture a wide variety of phenomena. We may, for example, be interested in estimating a temporal process that we think is smooth in time. In which case we could use a radial basis function such as the squared exponential,

\[c(x, x') = \sigma^2 \mbox{exp}(-\frac{|x - x'|_2^2}{\ell^2}).\]

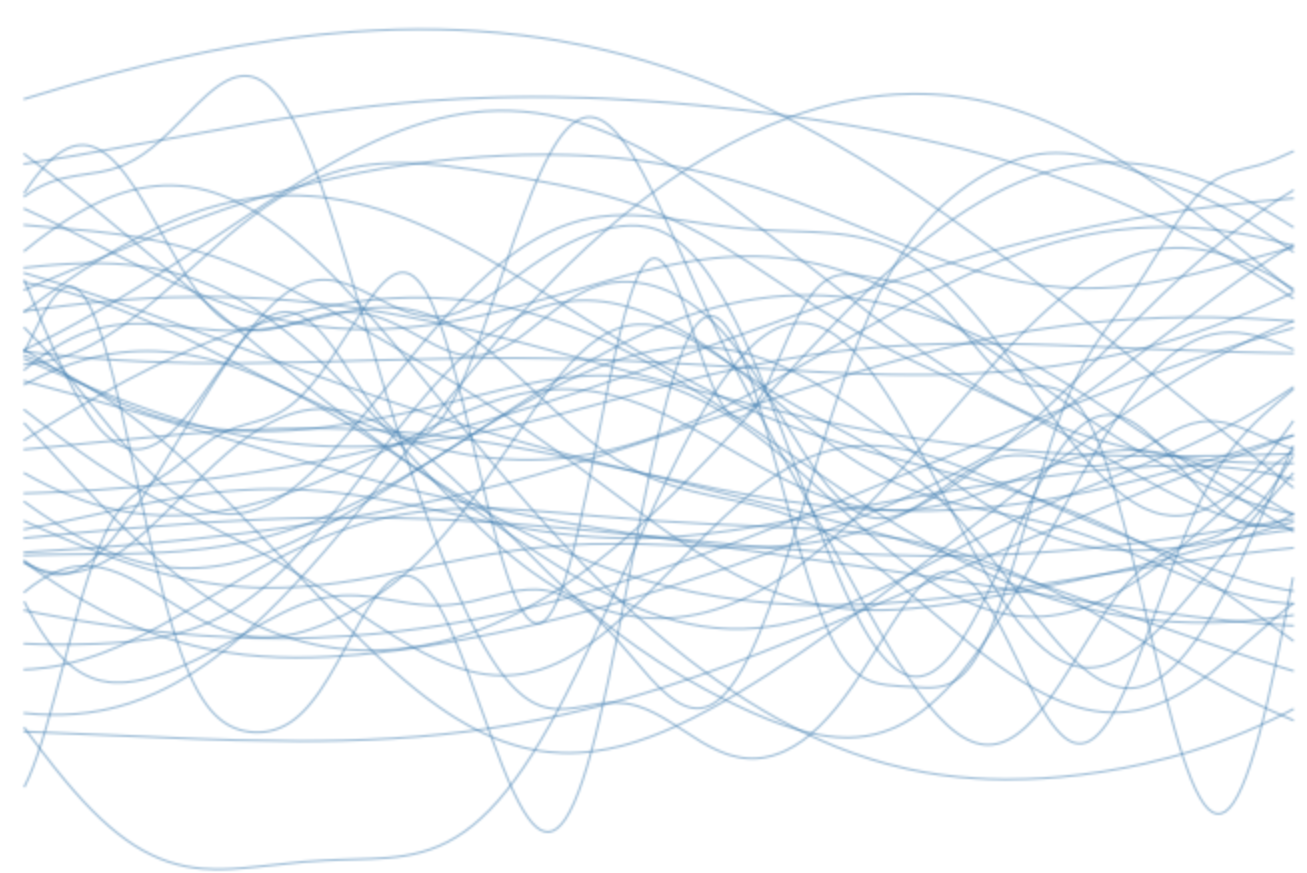
Samples from a Gaussian process prior using a squared exponential covariance function with various length scales.

Covariance functions can capture constant offsets, \(c(x, x') = a\), linear trends, \(c(x, x') = x * x'\), as well as countless other interactions. Covariance functions can be composed using sums, products and convolutions allowing you to define simple functions describing a single phenomena, then combine them with other functions to produce a more powerful model. Some of the more complex parts of the albatross code base are generic tools for composing and evaluating covariance functions. Choosing the covariance function (and associated hyper parameters) can be the hardest part and is very application specific and not in the scope of this document, so for what follows we will assume a valid covariance function has been provided.

Building a Gaussian Process

Given a covariance function, \(c(x, x')\) we can build our prior at the observed locations, \(x = \left[x_0, \cdots, x_n\right]\), by evaluating the function for each pair of locations,

\[\begin{split}\mbox{Cov}[ \mathbf{y} ] = \Sigma_{yy} = \begin{bmatrix}c(x_0, x_0) & c(x_0, x_1) & \cdots & c(x_0, x_n) \\ c(x_1, x_0) & c(x_1, x_1) & & \vdots \\ \vdots & & \ddots & \vdots\\ c(x_n, x_0) & \cdots & \cdots & c(x_n, x_n) \end{bmatrix}\end{split}\]

Doing a similar operation with the mean function, \(m(x)\), gives us the prior distribution for our measurements,

\[\begin{split}\begin{bmatrix} \mathbf{y}_0 \\ \vdots \\ \mathbf{y}_n \end{bmatrix} \sim \mathcal{N}\left(\begin{bmatrix} m(x_0) \\ \vdots \\ m(x_n) \end{bmatrix}, \begin{bmatrix} c(x_0, x_0) & \cdots & c(x_0, x_n) \\ \vdots & & \vdots \\ c(x_n, x_0) & \cdots & c(x_n, x_n) \\ \end{bmatrix} \right)\end{split}\]

or more concisely,

\[\mathbf{y} \sim \mathcal{N}\left(\mu_y, K_{yy}\right)\]

At its core that’s all there is to a Gaussian process. It’s just a way of describing how to create multivariate Gaussian distributions for arbitrary data, the process of fitting and predicting are just manipulations of Multivariate Gaussian Distributions.

Making Predictions

We now have all the tools we need to fit and predict with a Gaussian process. We can use the covariance function to build a multivariate Gaussian distribution which includes both our prior for our measurements \(\mathbf{y}\) and the unknown function values , \(\mathbf{f} ^* = \mbox{p}[f(x^*)]\),

\[\begin{split}\left[\begin{array}{c} \mathbf{y} \\ \mathbf{f} ^* \end{array}\right] \sim \mathcal{N}\left(0, \left[ \begin{array}{cc} K_{yy} & K_{y*} \\ K_{*y} & K_{**} \end{array}\right]\right)\end{split}\]

Making a prediction then consists of forming the conditional distribution of \(\mathbf{f} ^*\) given our measurements \(y \leftarrow \mathbf{y}\),

(1)\[ \mathbf{f} ^*|y \sim \mathcal{N}\left( K_{*y} K_{yy}^{-1} y \hspace{0.1cm}, \hspace{0.1cm} K_{**} - K_{*y} K_{yy}^{-1} K_{y*} \right)\]

That’s it. You provide a covariance function, measurements \(y\) at locations \(x\) and computing the conditional distribution will produce predictive distributions \(\mathbf{f^*}\) for arbitrary new locations, \(x^*\).

Fitting a Model

A naive approach to fitting (or training) would be to simply store \(c(x, x')\), \(y\) and \(x\) then for each desired prediction compute the posterior distribution. While such an approach would be extremely memory efficient (two vectors \(x\) and \(y\) so \(\mathcal{O}(2n)\) storage) it would result in repeated computation of \(K_{yy}^{-1}\) which requires \(\mathcal{O}(n^2)\) evaluations of the covariance function and \(\mathcal{O}(n^3)\) floating point operations for the inverse.

Instead we can decompose \(K_{yy}\) which will accelerate subsequent predictions. One such way to front load computation involves computing the Cholesky decomposition of \(K_{yy}\),

\[L L^T = K_{yy}\]

and the information vector,

\[v = K_{yy}^{-1} y.\]

After which a prediction can be made using,

\[ \begin{align}\begin{aligned}\label{eq:cholesky_prediction}\\ \mathbf{f^*} |y \sim \mathcal{N}\left( K_{*y} v \hspace{0.1cm}, \hspace{0.1cm} K_{**} - A^T A \right)\end{aligned}\end{align} \]

with

\[A = L^{-1} K_{y*}\]

Such an approach will require storing \(L\), and \(v\) resulting in \(\mathcal{O}(n^2)\) storage, but reduces the computation cost when predicting.

The Cholesky decomposition isn’t particularly stable unless you do pivoting. As a result the albatross implementation uses the LDLT decomposition,

\[P^T L D L^T P = K_{yy}\]

where \(P\) is a permutation matrix that holds the ordering used after pivoting and \(D\) is a diagonal matrix. This leads to a slightly different \(A\),

\[A = D^{-1/2} L^{-1} P K_{y*}\]

but otherwise all the math is the same. This LDLT approach is what we use in albatross when you build a Gaussian process in albatross and fit the model,

auto model = gp_from_covariance(k);
RegressionDataset<> dataset(x, y);
auto fit_model = model.fit(dataset);

Predictive Distribution

Once we’ve fit a model we can use it to make a prediction at arbitrary locations (called features in albatross), \(\mathbf{x}^*\),

\[\mathbf{f^*}|y \sim \mathcal{N}\left(K_{*f} K_{ff}^{-1} y, K_{**} - K_{*f} K_{ff}^{-1} K_{f*}\right)\]

Instead of computing this all from scratch, we use the precomputed quantities from the fit step. In particular we would write this,

\[\begin{split}\mathbf{f^*}|y & \sim \mathcal{N}\left(K_{*f} v, K_{**} - K_{*f} (P^TLDL^TP)^{-1} K_{f*}\right) \\ & \sim \mathcal{N}\left(K_{*f} \mathbf{v}, K_{**} - (K_{*f} P^T L^{-T} D^{-1/2}) (D^{-1/2}L^{-1}P K_{f*}\right) \\ & \sim \mathcal{N}\left(K_{*f} \mathbf{v}, K_{**} - Q_{f*}^T Q_{f*}\right)\end{split}\]

Where \(Q_{f*} = D^{-1/2}L^{-1}P K_{*f}^T\).

To make a prediction in albatross you’d first fit the model (see above), then call,

const auto prediction = fit_model.predict(new_features);

This predict call is actually a lazy operation (nothing is actually computed yet). You then have some choices for the actual prediction type you’d like:

Mean Predictions

Calling:

const Eigen::VectorXd mean = prediction.mean();

would:

• Evaluate \(K_{*f}\)

• Compute the mean \(K_{*f} v\)

Marginal Predictions

Calling:

const MarginalDistribution marginal = prediction.marginal();

would:

• Compute \(Q_{f*} = D^{-1/2}L^{-1}P K_{*f}^T\)

• Evaluate the prior variance \(\mbox{diag}(K_{**})\)

• Compute the posterior variance \(\mbox{diag}(K_{**}) - \mbox{diag}(Q_{f*}^T Q_{f*})\)

Joint Predictions

Calling:

const JointDistribution marginal = prediction.joint();

would:

• Evaluate the prior covariance \(K_{**}\)

• Compute the posterior covariance \(K_{**} - Q_{f*}^T Q_{f*}\)